Sections

General

In StructuralCodes, a Section is responsible for connecting a geometry object with an API for performing calculations on the geometry.

The section contains a SectionCalculator which contains the API for doing calculations on the geometry, including for example lower level methods for integrating a strain profile to stress resultants, or calculating a strain profile based on stress resultants, or higher level methods like calculating a moment-curvature relation, or an interaction diagram between moments and axial force.

The SectionCalculator uses a SectionIntegrator to integrate the strain response on a geometry.

The generic beam section

The GenericSection takes a SurfaceGeometry or a CompoundGeometry as input, and is capable of calculating the response of an arbitrarily shaped geometry with arbitrary reinforcement layout, subject to stresses in the direction of the beam axis.

In the example below, we continue the example with the T-shaped geometry.

Tip

If you are looking for the gross properties of the section, these are available at the .gross_properties property on the Section object ✅

Since the axial force and the moments are all relative to the origin, we start by translating the geometry such that the centroid is alligned with the origin.

Notice how we can use .calculate_bending_strength() and .calculate_limit_axial_load() to calculate the bending strength and the limit axial loads in tension and compression.

Furthermore, we have the following methods:

.integrate_strain_profile()

Calculate the stress resultants for a given strain profile.

.calculate_strain_profile()

Calculate the strain profile for given stress resultants.

.calculate_moment_curvature()

Calculate the moment-curvature relation.

.calculate_nm_interaction_domain()

Calculate the interaction domain between axial load and bending moment.

.calculate_nmm_interaction_domain()

Calculate the interaction domain between axial load and biaxial bending.

.calculate_mm_interaction_domain()

Calculate the interaction domain between biaxial bending for a given axial load.

See the GenericSectionCalculator for a complete list.

Syntax
Create a section and perform calculations.
from structuralcodes.sections import GenericSection

# Create a section
section_not_translated = GenericSection(geometry=t_geom)

# Use the centroid of the section, given in the gross properties, to re-allign
# the geometry with the origin
t_geom = t_geom.translate(dy=-section_not_translated.gross_properties.cz)
section = GenericSection(geometry=t_geom)

# Calculate the bending strength
bending_strength = section.section_calculator.calculate_bending_strength()

# Calculate the limit axial loads
limit_axial_loads = section.section_calculator.calculate_limit_axial_load()

# Calculate the interaction domain between axial force and bending moment
nm = section.section_calculator.calculate_nm_interaction_domain()

# Calculate the moment-curvature relation
moment_curvature = section.section_calculator.calculate_moment_curvature()

Notice how for example .calculate_moment_curvature() returns a custom dataclass of type MomentCurvatureResults. If we inspect this class further, we find among its attributes chi_y and m_y. These are the curvature and the moment about the selected global axis of the section. We also find the curvature and moment about the axis orthogonal to the global axis chi_z and m_z, and the axial strain at the level of the global axis eps_axial. All these attributes are stored as arrays, ready for visualization or further processing.

Tip

Use your favourite plotting library to visualize the results from the GenericSectionCalculator. The code below shows how to plot the moment-curvature relation in the figure below with Matplotlib. Notice how we are plotting the negative values of the curvatures and moments due to the sign convention.

Syntax
Visualize the moment-curvature relation.
import matplotlib.pyplot as plt

# Visualize moment-curvature relation
fig_momcurv, ax_momcurv = plt.subplots()
ax_momcurv.plot(
    -moment_curvature.chi_y * 1e3, -moment_curvature.m_y * 1e-6, '-k'
)
ax_momcurv.grid()
ax_momcurv.set_xlabel(r'$\chi_{\mathrm{y}}$ [1/m]')
ax_momcurv.set_ylabel(r'$M_{\mathrm{y}}$ [kNm]')
ax_momcurv.set_xlim(xmin=0)
ax_momcurv.set_ylim(ymin=0)
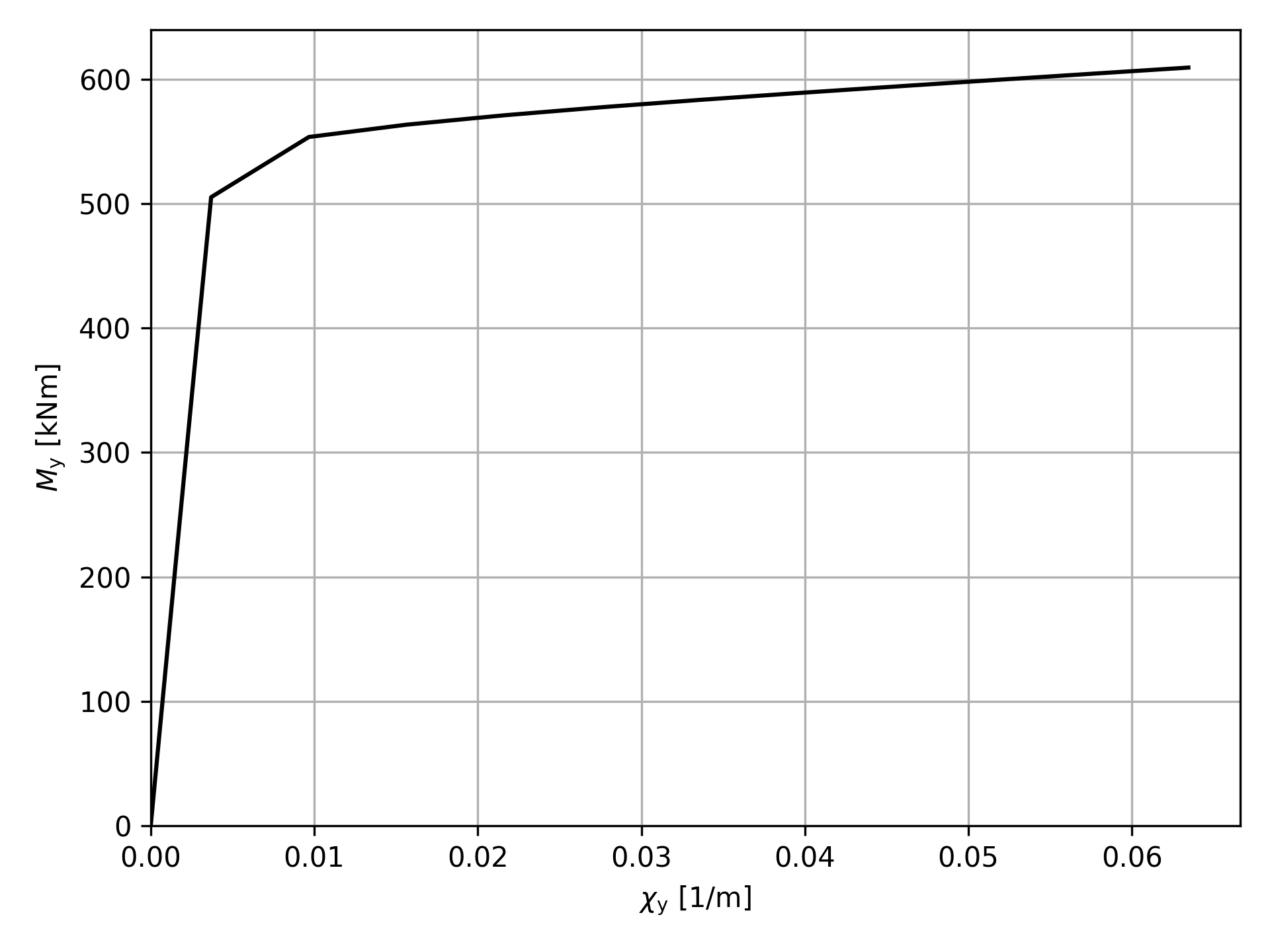
../../_images/moment_curvature.png

The moment-curvature relation computed with the code above.